Definition
Elastizitätsmodul E (Abkürzung E-Modul)
Der Elastizitätsmodul E ist ein Materialkennwert, der den Zusammenhang zwischen Spannung und Dehnung bei der Verformung eines festen Körpers bei linear elastischem Verhalten beschreibt. Er definiert das Verhältnis des Spannungsanstiegs und der dabei zunehmenden Dehnung bei unbeeinflusster Querschnittsverformung des Prüfkörpers. Der Elastizitätsmodul wird mit E-Modul oder als Formelzeichen mit "E" abgekürzt und hat die Einheit einer mechanischen Spannung.
Man unterscheidet das Kurzzeit-E-Modul, bestimmt im Zugversuch (nach DIN EN ISO 527-Teil 1) sowie das Langzeit E-Modul bzw. Kriechmodul, bestimmt im Biegeversuch (nach DIN EN ISO 178) und Zugversuch (siehe Bild 1).
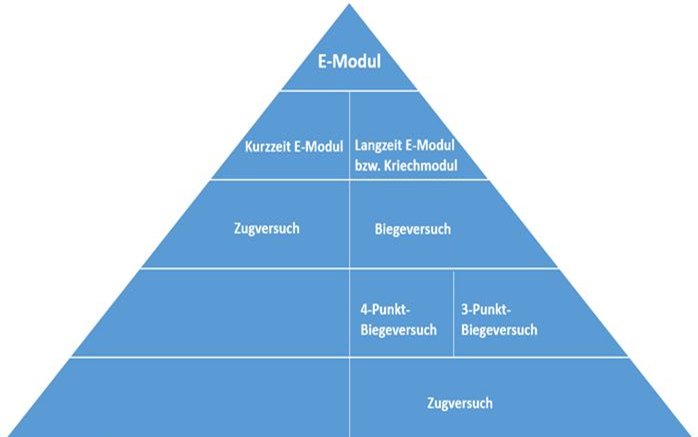
Bild 1: Übersicht der mechanischen Prüfverfahren zur Bestimmung des E-Moduls
Quelle: DIN Berlin
Seine experimentelle Ermittlung erfolgt unter einachsiger Belastung, wobei die Probekörper sowohl reiner Zug- als auch Biegezugbeanspruchung ausgesetzt sein können. Der E-Modul wird werkstoffspezifisch in einem Spannungs-Dehnungs-Diagramm (siehe Bild 2) dargestellt. Der E-Modul von Kunststoffen ist im Vergleich zu Metall deutlich geringer, kann jedoch durch die Zugabe von Verstärkungsfasern deutlich erhöht werden. Zu beachten ist jedoch, dass das Festigkeits-/Gewichtsverhältnis von Kunststoff in vielen Fällen nahe an das von Metallen herankommt. Der E-Modul bezeichnet den Steifigkeitsfaktor eines Kunststoffes, als im ideal-elastischen Anfangsbereich seiner Spannungs-Dehnungskurve und wird in N/mm2 oder MPa (1N/mm2 = 1 MPa) ausgedrückt. Der Betrag des E-Moduls ist umso größer, je mehr Widerstand ein Werkstoff seiner Verformung entgegensetzt. Ein Rohrsystem mit hohem E-Modul (z. B. aus Gusseisen) ist also steif (biegesteif), ein Rohrsystem mit niedrigem E-Modul (z. B. PP, PE) ist nachgiebig (biegeweich).
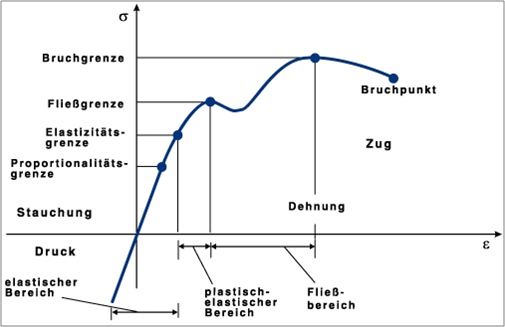
Bild 2: Allgemeines Spannungs-Dehnungs-Diagramm von Kunststoffen
In der Technik ist es häufig von großer Bedeutung, die Eigenschaften eines verwendeten Werkstoffs hinsichtlich seiner Festigkeit, seiner Plastizität bzw. seiner Sprödigkeit, seiner Elastizität und einiger anderer Eigenschaften genau zu kennen. Zu diesem Zweck werden Materialproben im Zugversuch getestet, indem die Probe mit bekanntem Ausgangsquerschnitt in eine Zugprüfmaschine eingespannt und mit einer Zugkraft F belastet wird. Unter Erhöhung der Kraft wird diese dann über der verursachten Längenänderung ΔL grafisch dargestellt. Diese Kurve bezeichnet man als Kraft-Verlängerungs-Diagramm.
Um eine Messkurve zu erhalten, die nur von der Art und Struktur des geprüften Materials, also nicht von den geometrischen Abmessungen der Probe abhängt, verwendet man reduzierte Einheiten, d. h. die Längenänderung ΔL wird auf die Anfangslänge L0 und die Kraft F auf den senkrechten Querschnitt A des Körpers im undeformierten Zustand bezogen. Diese jetzt von der Probenform unabhängige Kurve nennt man Spannungs-Dehnungs-Diagramm (siehe Bild 2/3).
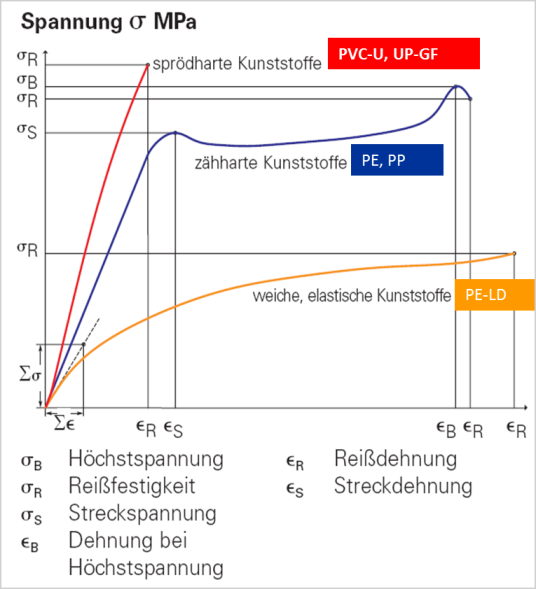
| Abkürzung | Beschreibung |
| σ S (Streckspannung) | Zugspannung, bei der die Steigung der S/D-Kurve erstmals den Wert 0 annimmt. |
| σ B (Höchstspannung) | maximale Zugspannung bei Höchstkraft |
| σ R (Zugfestigkeit bzw. Reißfestigkeit) | Zugspannung im Augenblick des Bruchs |
Bild 3: Spannungs-Dehnungs-Diagramm für sprödharte, zähharte und weiche, elastische Kunststoffe
Vergleicht man die Spannungs-Dehnungsdiagramme verschiedener Kunststoffe, kann man folgende Klassifizierung vornehmen:
- Spröde Werkstoffe haben eine hohe Festigkeit und eine geringe Reißdehnung.
Es existiert keine ausgeprägte Streckgrenze; Versagen tritt ohne Fließen auf. z. B. Duroplaste (auch faserverstärkt): Phenolharz, Polyesterharz, Epoxidharz; amorphe Thermoplaste wie z. B. Polyvinylchlorid-hart (PVC-U), Polystyrol (PS), Polymethylmethacrylat (PMMA) - Duktile (zähe) Werkstoffe haben eine Streckgrenze. Bei Beanspruchung oberhalb der Streckspannung kommt es zum Fließen bis zum Erreichen der Zugfestigkeit bzw. der Bruchspannung. Z. B. Polyoxymethylen (POM), Polycarbonat (PC), Polyamid (PA), Polypropylen (PP), Polyethylen hoher Dichte (PE-HD)
- Kautschukähnliche (gummiartige) Werkstoffe haben eine geringe Festigkeit mit sehr hoher Reißdehnung. Z. B. Polyvinylchlorid-weich (PVC-P), Polyethylen niedriger Dichte (PE-LD)
Erklärung der Spannungs-Dehnungskurve am Beispiel von Polyethylen PE
Der Kunststoff PE dehnt sich zunächst elastisch (Hook´scher Bereich), bei zunehmender Spannung und weiter zunehmender Verformung wird die Streckgrenze an einem Punkt σS irreversibel überschritten, wodurch sich der Werkstoff plastisch dehnt und schließlich versagt. Man stellt sich vor, dass die Moleküle der amorphen Bereiche von einer verknäuelten in eine mehr und mehr parallele (kristalline) Anordnung übergehen, schließlich aneinander entlanggleiten bis sie zuletzt den Kontakt zueinander verlieren.
Bei Kunststoffrohren tritt ein solches Versagen am Ort der geringsten Wanddicke auf und zwar durch eine Ausbeulung (Verformungsbruch). Bei diesem Erscheinungsbild liegt die Belastung (Spannung) oberhalb der mechanischen Festigkeit des Werkstoffes Polyethylen. Diese Bruchbild liegt dem ersten (flachen) Teil der Zeitstandskurven zugrunde. Zur Vermeidung eines solchen Schadensbildes bedarf es der richtigen Dimensionierung der Rohrleitung.
Analogiemodelle für die Spannungs-Dehnungs-Kurven (Zugbeanspruchung)
Unter der Einwirkung äußerer Kräfte kann die Verformung von Kunststoffen aus drei Anteilen bestehen.
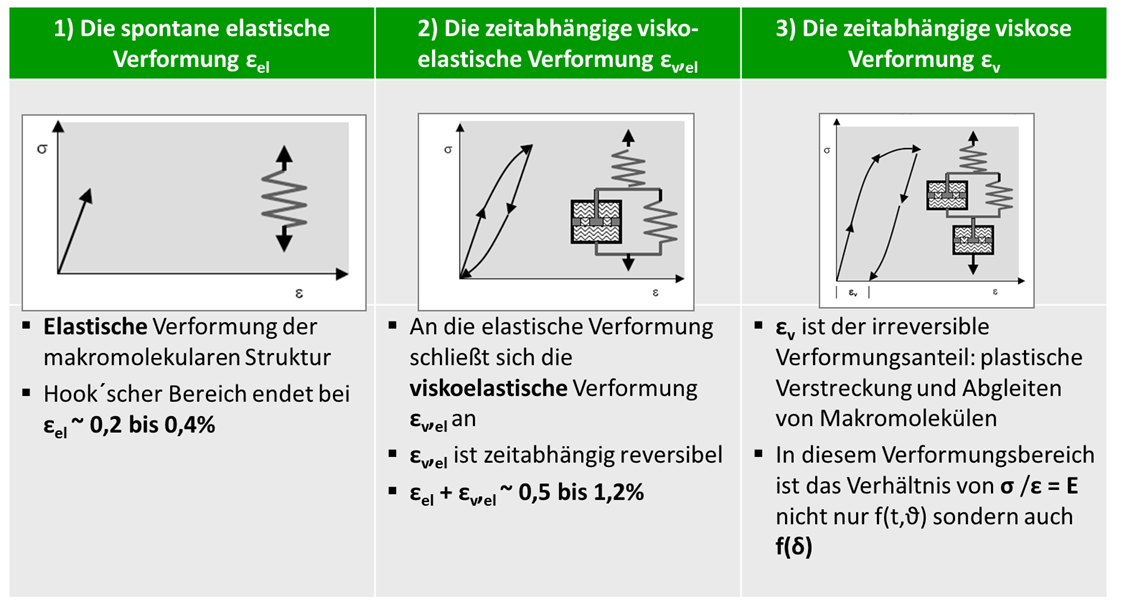
Bild 4: Analogiemodelle für die Spannungs-Dehnungs-Kurven (Zugbeanspruchung)
Das Hooke´sche Gesetz (nach Sir Robert Hooke) beschreibt das elastische Verhalten von Festkörpern, deren elastische Verformung/ Dehnung annähernd proportional zur einwirkenden Belastung/ Spannung ist, durch einen streng linearen Zusammenhang (linear-elastisches Verhalten). Dieses Verhalten ist z. B. typisch für Metalle bei kleinen Belastungen sowie für harte, spröde Stoffe oft bis zum Bruch (Glas, Keramik, sprödharte Kunststoffe wie PVC-U, GFK).

